1. 논문 개요
이 논문은 그래프 구조를 갖는 데이터(예: 논문 인용 네트워크, SNS 네트워크)에서 노드 분류(node classification) 문제를 풀기 위해 제안된 모델인 Graph Convolutional Network(GCN)을 다룹니다.
기존의 그래프 기반 학습법들이 갖는 한계 — 예컨대 그래프 구조와 노드 특징(feature)을 통합해서 학습하기 어렵다는 점 — 을 해결하는 방식으로, 그래프 위에 신경망 형태의 레이어 전파 규칙을 제시한 것이 특징입니다.
논문의 주요 기여는 다음과 같습니다:
- 그래프 합성곱(spectral graph convolution)의 1차 근사(first-order approximation) 를 이용해 계산량을 줄인 단순하면서도 강력한 레이어 규칙 제시
- 해당 구조를 이용해 실제 반지도 학습(semi-supervised) 환경에서 좋은 성능을 보였다는 실험 결과 제시
- 그래프 + 노드 특징을 동시에 이용하는 신경망 설계 방향을 제시
2. 배경 및 Motivation
논문이 다루는 문제 설정은 다음과 같습니다:
- 각 노드가 특징 벡터(feature)를 가지고 있고, 그래프의 엣지(adjacency) 정보 또한 주어진다.
- 일부 노드에는 레이블(label)이 있고, 나머지 노드는 레이블이 없다.
- 목표는 레이블이 없는 노드의 레이블을 예측하는 것이다 (반지도 학습).
- 이때, 노드의 특징만 보는 것보다 노드 간의 연결 정보(이웃 정보) 를 이용하면 성능이 향상될 수 있다.
- 기존 방식들은 그래프 라플라시안(Laplacian)을 이용한 정규화나 임베딩 기반 방식 등이 존재했지만, “깊은 신경망 레이어” 형태로 그래프 구조를 직접 다루는 방식은 부족했다.
이러한 왜곡을 해결하기 위해 논문에서는 그래프 구조의 합성곱 개념을 신경망 레이어 형태로 바꿔 제안합니다.
3. 모델 설명 — 핵심 수식 & 계산 흐름
3.1 레이어 전파 규칙
논문에서 제안된 기본 전파 규칙은 다음과 같습니다:
H(l+1)=σ(D~−12 A~ D~−12 H(l) W(l))H^{(l+1)} = \sigma\bigl(\tilde D^{-\tfrac12} \,\tilde A\, \tilde D^{-\tfrac12}\, H^{(l)}\, W^{(l)}\bigr)H(l+1)=σ(D~−21A~D~−21H(l)W(l))
여기서 각 기호는 다음을 의미합니다:
- H(l)H^{(l)}H(l): lll번째 레이어에서의 노드 표현 행렬 (크기 N×DlN \times D_lN×Dl)
- H(0)=XH^{(0)} = XH(0)=X: 입력 노드 특징 행렬 (크기 N×FN \times FN×F)
- AAA: 원본 인접행렬 (크기 N×NN \times NN×N)
- INI_NIN: 단위행렬 (자기자신과의 연결, self-loop)
- A~=A+IN\tilde A = A + I_NA~=A+IN: 자기 루프를 포함한 인접행렬
- D~\tilde DD~: A~\tilde AA~의 차수(degree) 대각 행렬, D~ii=∑jA~ij\tilde D_{ii} = \sum_j \tilde A_{ij}D~ii=∑jA~ij
- W(l)W^{(l)}W(l): 학습 가능한 가중치 행렬 (크기 Dl×Dl+1D_l \times D_{l+1}Dl×Dl+1)
- σ(⋅)\sigma(\cdot)σ(⋅): 활성화 함수 (예: ReLU)
그래프 구조를 반영하기 위해 D~−12 A~ D~−12\tilde D^{-\tfrac12}\,\tilde A\,\tilde D^{-\tfrac12}D~−21A~D~−21 형태의 정규화된 인접행렬이 사용됩니다.
이 정규화는 깊은 레이어에서 발생할 수 있는 학습 불안정이나 수치 문제(예: 그래디언트 폭발 또는 소멸)를 완화하는 역할을 합니다.
3.2 2-레이어 GCN 예시
논문에서는 실제로 다음과 같은 2-레이어 모델을 제시합니다:
Z=softmax(A^ ReLU(A^ X W(0)) W(1))Z = \mathrm{softmax} \bigl( \hat A \;\mathrm{ReLU}(\hat A\,X\,W^{(0)})\,W^{(1)} \bigr)Z=softmax(A^ReLU(A^XW(0))W(1))
여기서 A^=D~−12A~ D~−12\hat A = \tilde D^{-\tfrac12} \tilde A\,\tilde D^{-\tfrac12}A^=D~−21A~D~−21.
즉
- 우선 입력 특징 XXX에 A^\hat AA^를 곱해 이웃 노드 정보를 흡수하고, W(0)W^{(0)}W(0)를 곱한 뒤 ReLU 활성화.
- 다시 A^\hat AA^를 곱해 두 단계 이웃 정보를 어느 정도 반영하고, W(1)W^{(1)}W(1)를 곱한 뒤 softmax를 적용해 각 노드의 레이블 확률 ZZZ를 구함.
이 구조가 반지도 학습 환경에서 효과적으로 작동함을 여러 데이터셋에서 보여줍니다.
3.3 직관적 흐름
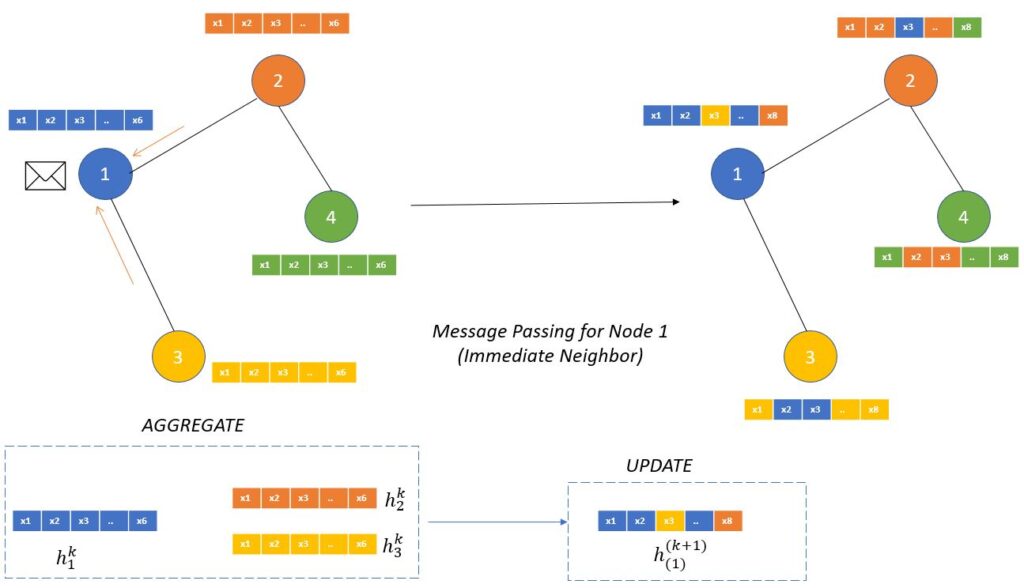
- 각 노드는 자신의 특징뿐 아니라 연결된 이웃 노드들의 특징도 흡수하면서 표현이 갱신됩니다.
- 첫 레이어는 “직접 이웃(1-hop) 정보”를 모으고, 다음 레이어를 통해 약간 더 먼 거리에 있는 이웃(2-hop) 정보까지 반영 가능해집니다.
- 이러한 방식으로, 그래프의 구조와 노드 특징이 섞여서 더 풍부한 표현(representation)을 얻게 됩니다.
4. 논문의 장점 및 인사이트
✅ 장점
- 구조적 정보 반영: 단순히 노드의 특징만 보는 것이 아니라, 그래프 연결 구조(이웃 관계)를 깊이 있게 활용합니다.
- 계산 효율성: 스펙트럴 그래프 합성곱을 복잡하게 구현하는 대신, 1차 근사를 도입해 실제 학습 가능한 형태로 단순화했습니다.
- 실험적 검증: 여러 그래프 노드 분류 데이터셋(Cora, Citeseer, PubMed 등)에서 우수한 성능을 보였습니다.
- 설계 단순성: 복잡한 하이퍼파라미터 없이 구조가 비교적 간단해서 이해하기 좋습니다.
💡 인사이트
- 이 논문을 통해 “그래프 + 신경망” 융합의 기본 틀이 자리잡았습니다. GCN 이후 많은 그래프 신경망(GNN: Graph Neural Network)이 이 구조를 바탕으로 확장되었습니다.
- “이웃의 정보 흡수”라는 개념이 자연스럽게 메시지 패싱(message passing) 관점에서 재정립되었고, 이후 모델들이 이 패러다임을 활용합니다.
5. 논문의 한계 및 주의사항
⚠️ 한계
- Full-batch 학습 방식: 논문 모델은 전체 그래프를 한꺼번에 들여와 학습하는 방식으로, 매우 큰 그래프의 경우 메모리/연산 측면에서 부담이 될 수 있습니다.
- 깊이 확장성의 제약: 레이어 수를 많이 쌓을 경우 “oversmoothing”(모든 노드 표현이 비슷해지는 현상) 문제가 발생할 수 있습니다.
- 엣지 특징 미지원: 노드 간의 연결에 대한 가중치(edge weight)나 방향(directed edge) 또는 엣지의 추가 특징(edge feature)을 자연스럽게 다루지는 않습니다.
- 무향 그래프 기반: 기본적으로 논문에서는 무향(undirected) 그래프를 가정하고 있으므로, 방향성이 강한 그래프에는 추가 설계가 필요합니다.
🔍 주의사항
- 그래프의 규모가 매우 큰 경우에는 미니배치(mini-batch) 기반의 샘플링 방법(예: GraphSAGE)이나 인접행렬의 희소 표현(sparse representation)을 고려해야 합니다.
- 그래프 구조가 매우 복잡하거나 노드 간 이질성이 크다면, 단순 GCN 구조보다 애드혹(ad-hoc) 한 설계가 필요할 수 있습니다 (예: 엣지 특징, 방향성, 노드군집화 등).
6. 느낀 점 및 적용 가능성
- 개인적으로 이 논문을 읽으면서 “그래프 데이터에서도 신경망처럼 층(layer)을 쌓을 수 있구나” 라는 인사이트가 강하게 왔습니다.
- 특히 SNS, 추천시스템, 지식그래프, 생물학 네트워크 등 노드 + 연결 구조가 명확한 영역에서 GCN은 매력적인 모델입니다.
- 다만 실제 적용 시에는 데이터 특성(노드 수, 엣지 수, 특징 벡터 크기), 학습 리소스, 그래프의 동적 변화 여부 등을 면밀히 고려해야 합니다.
- 이후에는 이 논문의 구조를 바탕으로 좀 더 최신 모델(예: Graph Attention Network(GAT), GraphSAGE 등)으로 확장해보는 것도 좋을 것 같습니다.